Definición de límite
Función simple
Función a trozos
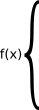
|
g(x) :, x < s
si s = h(x) :, x > s |
Opciones
Ayuda

Objetivo del applet
Entender la definición de límite de una función en un punto.
Datos de entrada
Dentro del applet: Los valores de Delta y Epsilon se pueden modificar moviendo los deslizadores. Los puntos A (punto donde se estudia el límite), C (punto donde cambia la definición a trozos) y L (posible límite) pueden variarse si los arrastramos con el ratón.
Función simple: Introducir la expresión dependiente de 'x' y pulsar 'Enter' para que se actualice la gráfica
Función definida a trozos: Se trata de una función compuesta por dos tramos (las funciones g y h) y un punto intermedio(C(t,s)). Estos componentes se pueden definir de la misma forma que la función simple.
Opciones: Se puede ocultar/mostrar la rejilla, las franjas asociadas epsilon - delta.
Datos de salida
La gráfica representa las funciones según se desee mostrando bien la función simple o la definida a trozos
Existen etiquetas informativas de la definición de éstas y el valor del punto A en tiempo real
Primeros pasos
Consideramos f dada por f(x)=(x+1)/(x-1). En el punto A=2 para epsilon = 1, busca un delta de modo que los pares (x,f(x)) de la franja verde entren en la franja roja, para L=3. ¿Y si L=5?
Comprueba la definición de límite en el origen para la función a trozos del applet. A continuación, mediante el ratón desliza el punto C y trata de ver la existencia del límite.
Construye una función a trozos de modo que tenga límite en todo número real.