Definition of limit
Simple function
f(x) :
Piecewise function
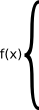
|
g(x) :, x < s
si s = h(x) :, x > s |
Options
Help
Show help


Aim of the applet
Understand the definition of limit of a function at a point.
Input data
- In the applet: The values of Delta and Epsilon can be modified by moving sliders. The points A (the point where we study the limit), C (point where it changes the definition to pieces) and L (possible limit) can be varied by dragging the mouse.
- Simple function: Enter the expression dependent of 'x' and press 'Enter' to update the graph.
- Piecewise function: This is a function composed of two sections (the functions g and h) and an intermediate point (C (t, s)). These components can be defined in the same way that the simple function.
- Options: You can hide / show the grid, the strip of epsilon and the strip of delta.
Output data
The graph represents the functions as desired, showing the simple function or piecewise.
There are informative labels from the definition of these and the value of point A in real time.
First steps
- We consider f given by f (x) = (x +1)/(x-1). At point A = 2 for epsilon = 1, find a delta so that the pairs (x, f (x)) of green strip to enter in red stripe, for L = 3. What happens if L = 5?
- Check the definition of the limit in the origin for the piecewise function of the applet. Then, slide the point C by the mouse and try to see the existence of the limit.
- Build a piecewise function such that the limit is a real number.