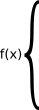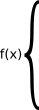Obxectivo do applet

Entender a definición de límite dunha función nun punto.

Datos de entrada

• Dentro do applet: Os valores de Delta e Epsilon pódense modificar movendo os deslizadores. Os puntos A (punto onde se estuda o límite), C (punto onde cambia a definición a anacos) e L (posible límite) poden variarse se os arrastramos co rato.
• Función simple: Introducir a expresión dependente de 'x' e pulsar 'Enter' para que se actualice a gráfica
• Función definida a anacos: Trátase dunha función composta por dous tramos (as funcións g e h) e un punto intermedio(C(t,s)). Estes compoñentes pódense definir da mesma forma que a función simple.
• Opcións: Pódese ocultar/amosar a reixa, as franxas asociadas epsilon - delta.

Datos de saída

A gráfica representa as funcións segundo se desexe mostrando ben a función simple ou a definida a anacos.

Existen etiquetas informativas da definición destas e o valor do punto A en tempo real.

Primeiros pasos

• Consideramos f dada por f(x) = (x+1)/(x-1). No punto A = 2 para epsilon = 1, busca un delta de modo que os pares (x,f(x)) da franxa verde entren na franxa vermella, para L = 3. E se L = 5?
• Comproba a definición de límite na orixe para a función a anacos do applet. A continuación, mediante o rato desliza o punto C e trata de ver a existencia do límite.
• Constrúe unha función a anacos de modo que teña límite en todo número real.